The effect of hyperbaric oxygen on the oxygen window

BY EDDIE BRIAN, JR., M.D.

The oxygen window. Inherent unsaturation. Partial pressure vacancy. Most divers with an interest in decompression diving have likely encountered one of these terms at some time. All three terms are used to describe the same physical phenomenon. For this article, the term oxygen window will be used, as it appears to be the most commonly applied term. However, the terms "inherent unsaturation" and "partial pressure vacancy" more correctly describe the physical phenomenon.

Current techniques of oxygen-facilitated decompression diving are based on use of the oxygen window. Despite common use of the oxygen window by divers, it appears to be one of the least- appreciated concepts in decompression diving. Understanding the oxygen window requires knowledge of circulatory and gas transport physiology, and the best place to start is with normobaric physiology.

LIFE AT ONE ATMOSPHERE
Physiology is not homogeneous. In healthy individuals under normal conditions, lung blood flow and ventilation, as well as tissue blood flow and metabolism, vary over wide ranges. Blood flow, ventilation and metabolism can vary both between individual areas and globally over time. These variables affect the precise gas exchange occurring in individual areas of the lungs and body tissues. To make these complex processes somewhat easier to understand, much of the physiology has been reduced to the simplest terms. However, the descriptions correctly reflect the global processes of gas uptake and elimination, and values presented represent average values. Partial pressure values are expressed in millimeters of mercury (mmHg), and 1 ATA equals 760 mmHg. For Systeme International purists, division by 7.5 converts mmHg to kilopascals, the correct SI unit of pressure.

Gas movement from lung to tissue and back is dependent on a partial pressure gradient. The concept of the partial pressure of a gas in solution is sometimes confusing, as gas in a liquid is dissolved in solution. A gas dissolved in liquid does not exert hydrostatic pressure like a gas in the gas phase, because the gas atoms or molecules are no longer free to move about as in the gas phase. This is an extremely important concept to understand or accept. The forces that hold a gas in solution are the same forces that hold any non-ionized solute (gas, liquid or solid) in solution. Tissues are principally liquids, and the partial pressure of a gas dissolved in a liquid is defined as the partial pressure that the gas would exert if the gas phase were in equilibrium with the liquid. Tissue gas partial pressures are commonly expressed as mmHg or atmospheres absolute (ATA). Tissue gas partial pressure is an index of the amount of gas present in the tissue. The total amount of gas present in a tissue is also affected by gas solubility, which can vary between gases and tissues. A tissue will absorb a larger volume of a highly soluble gas as opposed to a lower solubility gas before reaching any given partial pressure. In other words, if a given volume of gas dissolves in a tissue, the tissue partial pressure of a highly soluble gas will be lower than the tissue partial pressure of a low solubility gas.

Gas in solution moves by diffusion from an area of higher partial pressure to an area of lower partial pressure. Although the force for diffusion is a partial pressure gradient, it is not "pressure" per se that drives the movement of gas. When a gas line is pressurized to fill a cylinder, the pressure differential drives bulk movement of gas atoms or molecules. However, diffusion is not bulk movement of gas but rather the movement of individual gas atoms or molecules due to random atomic or molecular movement. Diffusion of an individual gas into or out of a tissue is dependent only on the partial pressure gradient of the gas, and not on other gases present in the tissue. This may seem paradoxical, as divers frequently conceptualize gases present in tissue as exerting a "pressure" that "holds" other gases out of the tissue. This analogy is incorrect. The diffusion of gases is not dependent on the bulk movement due to a pressure differential, but rather movement of individual gas atoms or molecules down the partial pressure gradient. The interaction of individual gases dissolved in solution does not affect diffusion of gases.

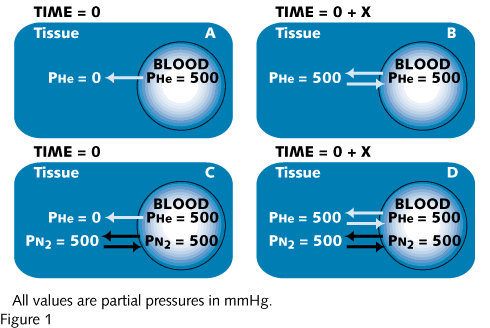
As an example, Figure 1 shows gas diffusion from blood into tissue. In Figure 1A, at time 0, blood with a helium (He) partial pressure (PHe) of 500 mmHg flows into a capillary in tissue with a PHe of zero. Due to random movement, He atoms begin to encounter the inner capillary wall. Some He atoms cross the capillary wall into tissue, where the He atoms can either diffuse further into tissue or diffuse back into the capillary. The direction of movement is a random event, but at this point there are many more He atoms encountering the capillary inner wall as opposed to the outer wall, and the overall He diffusion is out of the capillary. At some intermediate time point between Figures 1A and 1B, the tissue PHe would rise to 250 mmHg. At this point, He atoms in tissue would encounter the capillary outer wall with one-half the frequency that He atoms in blood would encounter the capillary inner wall. The overall He diffusion is still out of the capillary but at one-half the rate as in Figure 1A. Eventually at time 0 + X, equilibrium is reached and the PHe is 500 mmHg in both blood and tissue (Figure 1B). At equilibrium, He atoms continue to cross the capillary wall and diffuse into tissue at the same rate as when the tissue PHe was zero. However, the net diffusion of He atoms is now zero, because He atoms in tissue now encounter the capillary outer wall and diffuse back into the capillary at the same rate as He atoms encounter the capillary inner wall and diffuse into tissue (denoted by the arrows of the same length). In Figure 1C, a condition similar to Figure 1A exists except that blood and tissue have first been equilibrated with 500 mmHg partial pressure of nitrogen (PN2). The N2 is in equilibrium, and N2 molecules are diffusing out of and back into the blood at an equal rate. Assuming that ambient pressure is equal to or greater than 1000 mmHg, when blood with a PN2 of 500 mmHg and a PHe of 500 mmHg flows into the capillary, He diffuses into tissue as in Figure 1A. The N2 molecules do not block He diffusion from blood into tissue. The He diffusion gradient is 500 mmHg in both Figures 1A and 1C. In Figure 1D, He would reach equilibrium with the tissue in the same amount of time as it took for He alone to reach equilibrium in Figure 1B.

When a gas diffuses through a liquid, the interactions of the gas molecules with the liquid molecules predominate over any gas-gas interactions. As an example, if water is saturated with N2 at 1 ATA and 37¼ C, the N2 molecules are only 0.01% of the total molecules (water and N2). If the amount of N2 were doubled (2 ATA), then N2 molecules increase to only 0.02% of the total number of molecules. In reality, the chance of interaction between N2 and water molecules is greater than the above percentages would indicate, as the molecular diameter of water is larger than most gas molecules (water is a larger target). Furthermore, because of solvent-solute (water-gas) interactions, the dissolved gas molecules tend to remain surrounded by water molecules. The concept that gas atoms or molecules dissolved in tissue can "push" other gas molecules out of the tissue due to gas-gas interactions is not correct.

GAS TRANSPORT IN BLOOD
Under all conditions, blood that perfuses the lungs gives up CO2 and absorbs O2. Under normal conditions at 1 ATA, we are saturated with N2 and other trace gases, so there is no partial pressure gradient for these gases between lung and tissue. For most normobaric physiology, N2 and other trace gases are ignored, as there is no active exchange of these gases. For our purposes, it is helpful to include nitrogen and trace gases, as it helps illustrate how the oxygen window can be enlarged. In the following, all of the trace gases (principally argon) have been included with N2 to simplify the discussion and figures. Atmospheric CO2 has also been ignored as CO2 represents only a fraction of a percent of the atmosphere.

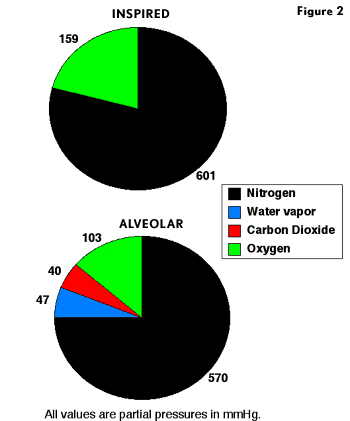
When we breathe air at 1 ATA, the inspired air moves down our respiratory tract where it reaches the alveoli, the gas exchange units of the lungs. As gas moves into our lungs, it becomes saturated with water vapor, diluting the inspired gases. At 37C, the partial pressure of water vapor is 47 mmHg. The membrane of the alveoli does not constitute a barrier to gas diffusion, and alveolar gases rapidly equilibrate with the blood traversing the alveolar capillary. Because alveoli are gas spaces in communication with ambient atmosphere, the sum of gas partial pressures in the alveoli must equal ambient pressure. Oxygen diffuses out and CO2 diffuses into alveoli, both processes lowering the O2 partial pressure (PO2) in alveoli. Figure 2 shows inspired and alveolar gas partial pressures for air. At 1 ATA, dry air has a PO2 of 159 mmHg. However, by the time air reaches an alveolus and equilibrates with blood, the alveolar PO2 (PAO2) has fallen to 103 mmHg. This means that the PO2 in blood perfusing the alveoli capillary cannot be higher than 103 mmHg. If all alveoli in the lungs had perfect ventilation and perfusion, the PO2 of arterial blood would be 103 mmHg. However, ventilation and perfusion in the lungs are not perfect, and under normal conditions in healthy individuals some blood traverses the lungs without undergoing gas exchange. All blood flowing though the lungs eventually mixes together in the left side of the heart. During mixing, the unventilated blood removes some oxygen from blood that underwent gas exchange, resulting in a further lowering of arterial PO2 (PaO2) to 95 mmHg. A PaO2 of 95 mmHg is an optimal value, and actual PaO2 values of healthy individuals may vary between 85 and 95 mmHg.

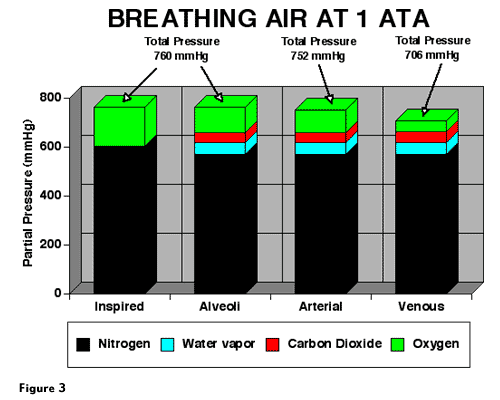
For practical purposes, liquids are incompressible and do not respond to changes in ambient pressure. Because of this, the sum of gas partial pressures in a liquid can be less than ambient pressure. Liquids such as blood and other body tissues will equilibrate only with the gas partial pressures to which they are exposed. On the alveolar side of the alveolar membrane, the total partial pressures must equal ambient pressure. However, on the liquid side of the membrane, the total partial pressures can be less, and in some areas may be quite a bit less than ambient pressure. The partial pressure that a gas exerts in a liquid depends on the temperature, the solubility of the gas in the liquid and the amount of gas present. Thus, if the amount of gas present and the temperature remain constant, the partial pressure of the gas in a tissue is fixed. If one gas is removed from a tissue, the remaining gases do not expand to fill the partial pressure vacated by the gas that was removed. Figure 3 shows total partial pressures for air breathing at 1 ATA from inspired gas to venous blood. Because of the decline in PO2 from alveoli to arterial blood, the total gas partial pressure in arterial blood during air breathing at 1 ATA is 752 mmHg, less than ambient pressure (760 mmHg). If PaO2 is lower than 95 mmHg (assumed in this example), then the total partial pressure in arterial blood will be less.

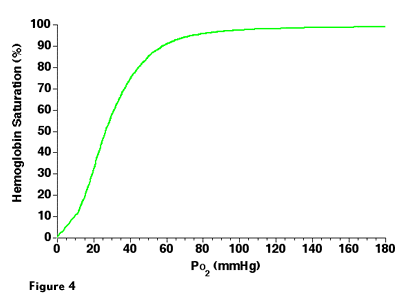
Metabolically inactive gases such as He and N2 are transported only in the dissolved phase in blood and the amount of gas present in blood is directly related to the gas partial pressure. In contrast, the metabolic gases O2 and CO2 have highly specialized transport systems. At 1 ATA, most O2 is transported in blood bound to hemoglobin. Hemoglobin is a specialized protein in red blood cells (RBCs) that reversibly bind O2. When O2 is bound to hemoglobin, it is no longer dissolved in solution and no longer contributes to the PO2. Because of O2 binding to hemoglobin, the relationship between the O2 content of blood (CO2) and PO2 is very non-linear due to the non-linear O2-hemoglobin disassociation curve (Figure 4). The vertical axis is the hemoglobin percent saturation, which represents the fraction of hemoglobin molecules that have O2 bound. The horizontal axis is the PO2. The left side of the curve is relatively steep, and as PO2 increases, the percent saturation rapidly increases as O2 is bound to hemoglobin. As hemoglobin saturation approaches 90%, the curve begins to flatten, and the increase in saturation becomes less for any increase in PO2. Under normal conditions, hemoglobin binds 1.39 mL O2 per gram of hemoglobin. In the following examples, a normal hemoglobin concentration of 15 grams of hemoglobin per deciliter (dL) of blood was assumed. The amount of O2 bound to hemoglobin can be calculated by multiplication of the hemoglobin concentration by 1.39 then multiplication by the hemoglobin saturation. For example, if the hemoglobin is 15 g/dL and saturation is 97.25%, then the O2 bound to hemoglobin is (1.39)(15)(0.9725) = 20.28 mL O2/dL blood. Oxygen also dissolves in blood, but the amount of dissolved O2 is small compared to the amount bound to hemoglobin. Only 0.003 mL O2/deciliter blood/mmHg PO2 will dissolve in blood. With 97.25% hemoglobin saturation, the PO2 is 95 mmHg, so the dissolved O2 is (0.003)(95) = 0.29 mL O2/dL blood. The CO2 of blood is the sum of the hemoglobin-bound fraction and the dissolved fraction. Thus, the CO2 is related to the PO2, but it is not a simple linear relationship as with gases that are purely dissolved. Carbon dioxide is also transported in states other than dissolved, being converted to bicarbonate ions inside of RBCs and by binding to hemoglobin. However, these mechanisms are much less efficient than the binding of O2 to hemoglobin; the relationship between the PCO2 and CO2 content (CCO2) is almost linear.

As blood perfuses tissue, O2 moves into tissue and CO2 moves into blood. If the PO2 absorbed from blood were replaced by an equal PCO2 from tissue, there would be no change in total partial pressure from the arterial to the venous blood. However, as blood traverses tissue, the increase in PCO2 is much less marked than the decrease in PO2. This is the genesis of the oxygen window. Breathing air under normal conditions at 1 ATA, the average arterial-venous (a-v) difference in PO2 is about 50 mmHg, meaning that venous PO2 (PvO2) is about 50 mmHg less than PaO2. As PO2 is reduced 50 mmHg, PCO2 increases only 5 mmHg from the arterial to venous blood. PCO2 increases much less than the decrease in PO2 due to two reasons. First, not all O2 consumed is converted to CO2. Under normal conditions, only 80% of O2 is converted to CO2. The second and more important reason is that CO2 is 20 times more soluble in blood than O2. Gases that are more soluble produce a lower partial pressure when a given volume of gas is absorbed into a liquid.

Figure 3 shows total gas partial pressures during air breathing at 1 ATA. The sum of the partial pressures declines slightly from the alveoli to arterial blood, where the total partial pressure is 752 mmHg. The total partial pressure present on the venous side of the circulation is 706 mmHg due to the consumption of O2 by tissue. In this example, O2 declines from 95 to 44 mmHg while CO2 increases from 40 to 45 mmHg. Nitrogen and water vapor partial pressures remain constant from the alveoli to arterial to venous circulation. Under normal conditions breathing air at 1 ATA, venous blood is undersaturated by 54 mmHg. This value was calculated by subtraction of the sum of the partial pressures in venous blood from ambient pressure. The oxygen window is opened when O2 is removed from arterial blood but only partially replaced by CO2 in venous blood. The principle factor in formation of the oxygen window is the a-v PO2 difference. The total gas partial pressure in tissue is less than venous blood due to the diffusion gradients between tissue and blood. PO2 decreases as the distance from a capillary increases, but PCO2 increases only slightly due to solubility of CO2.

Undersaturation of blood and tissues has been documented in several studies. In 1910, Krogh demonstrated that the total gas partial pressure in arterial blood was less than ambient pressure, although Krogh could not measure individual gas partial pressures (5). Since Kroghs time, inherent unsaturation of the venous blood and tissues has been confirmed by direct measurement of gas partial pressures in venous blood and tissue (1, 6). The findings of the experimental studies are consistent with calculated values presented in the figures in this article. The arterial-to-venous reduction in total gas partial pressure was later termed partial pressure vacancy by Momsen, inherent unsaturation by Hills, and the oxygen window by Behnke (7).

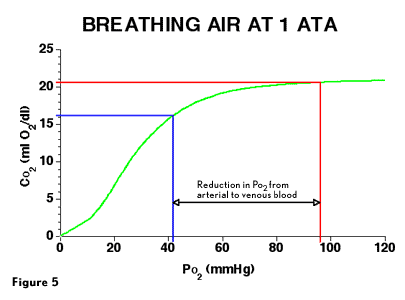
The precise size of the oxygen window depends upon the CaO2 and tissue oxygen consumption. Figure 5 shows the O2-hemoglobin disassociation curve, but the vertical axis is CO2 rather than percent hemoglobin saturation shown in Figure 4. The lines labeled arterial represent PaO2 and CaO2 and the lines labeled venous represent PvO2 and CvO2 during air breathing at 1 ATA. For this graph, an average a-v CO2 difference of 4.5 mL O2/dL blood and a hemoglobin concentration of 15 g /dL blood has been assumed. For any given PaO2, the CaO2 can be calculated, and CvO2 determined by subtraction of 4.5 mL O2/dL from the CaO2 value. PvO2 can then be determined from the curve by finding the PvO2 value that corresponds to the calculated CvO2. The total venous partial pressures can then be summed and subtracted from ambient pressure to determine the oxygen window. To determine the corresponding partial pressure and content values plotted on the O2-hemoglobin disassociation curves in these examples, a more precise O2-hemoglobin nomogram was used. The O2-hemoglobin disassociation curve flattens at higher PO2 values because hemoglobin is approaching 100% saturation, and any additional O2 is carried principally in the dissolved phase. Because the amount of O2 that will dissolve is much less than will bind to hemoglobin, when hemoglobin is fully saturated the increase in CO2 is much less for any increase in PO2. When O2 is transferred from blood into tissue, dissolved O2 diffuses from blood into tissue, and then is replaced by O2 released from hemoglobin.

As blood passes through tissue, a fixed volume (content) of O2 is removed. The change in PO2 required to supply the volume of O2 depends on where the CO2 values lie on the O2-hemoglobin disassociation curve. Because the slope of the O2-hemoglobin disassociation curve flattens on the right of the curve, as PaO2 moves to the right, the reduction in PO2 becomes greater when a fixed volume of O2 is removed. This is because a greater amount of dissolved O2 is being removed as you move to the right on the curve, meaning that the average change on the vertical axis is always 4.5 mL O2/dL, but the change on the horizontal axis varies depending on where the CO2 values lie along the curve. This is how the oxygen window is enlarged when PO2 is increased. Assuming that the volume of O2 removed is constant (4.5 mL O2/dL), then the amount of CO2 produced is constant, and the increase in PvCO2 is also constant. This means that the a-v increase in PCO2 is always about 5 mmHg, while the a-v PO2 reduction can vary from 50 to greater than 1000 mmHg.

LIFE BREATHING OXYGEN AT ONE ATMOSPHERE
Before moving into hyperbaric physiology, understanding how the oxygen window can be enlarged at 1 ATA is helpful in understanding the transition from surface to depth.

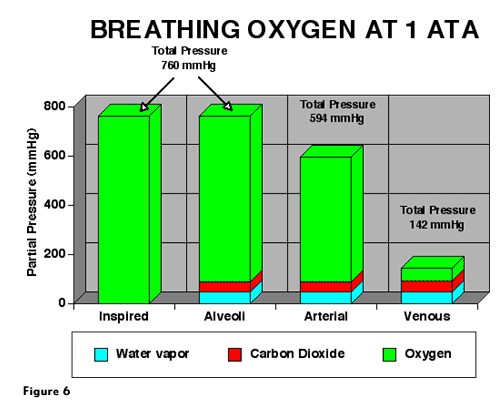
Figure 6 shows inspired to venous blood partial pressures during O2 breathing at 1 ATA. In this example, it is assumed that all nitrogen, argon and other trace gasses have been washed out of the system. During O2 breathing, the ventilation/perfusion inequalities in lung have a much greater impact on PaO2 than during air breathing. Under optimal conditions during O2 breathing at 1 ATA, PaO2 would be about 500 mmHg. Because of the greater difference between alveolar and arterial PO2, arterial blood is undersaturated by 166 mmHg. As blood moves through tissue, the same 4.5 mL O2/dL blood is extracted, and PO2 falls to 57 mmHg in venous blood. Thus, venous blood is unsaturated by 518 mmHg during O2 breathing at 1 ATA.

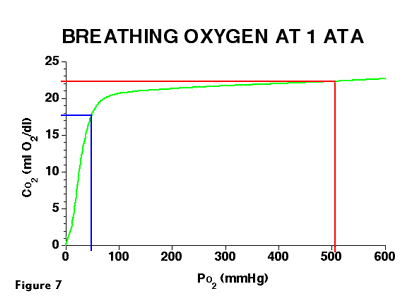
Figure 7 shows the a-v CO2 and PO2 differences during O2 breathing at 1 ATA. This is the same oxygen-hemoglobin disassociation curve shown in Figure 5, but the right side of the graph has been extended to greater PO2 values. Note that the amount of O2 removed is 4.5 mL O2/dL blood (on the vertical axis), the same as in Figure 5. However, because the PaO2 is moved far to the right where the slope of the curve is flat, the change in PO2 is much greater than air breathing at 1 ATA. In this example, the 518 mmHg unsaturation in venous blood is the oxygen window. If a non-respiratory gas were being evolved from tissue, it could occupy some or all of the window.

LIFE UNDER WATER
So finally we arrive at the effects of hyperbaric conditions on the oxygen window. Breathing O2 at 20 FSW results in an inspired PO2 of 1.6 ATA (1216 mmHg). As in the previous example of O2 breathing at 1 ATA, only respiratory gases were assumed to be present. Figure 8 shows inspired to venous gas partial pressures for O2 breathing at 1.6 ATA. As in previous Figures 3 and 6, there is a stair step decline in total partial pressures from the alveoli to venous blood.

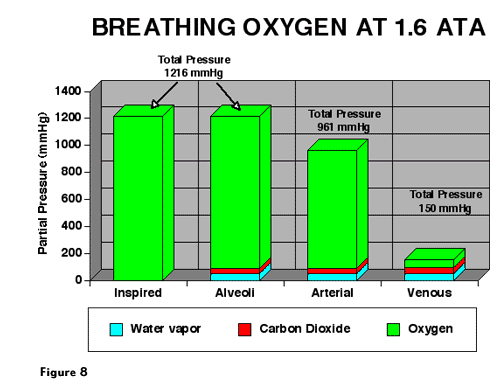
Figure 9 shows the relationship between CO2 and PO2 values for O2 breathing at 1.6 ATA.

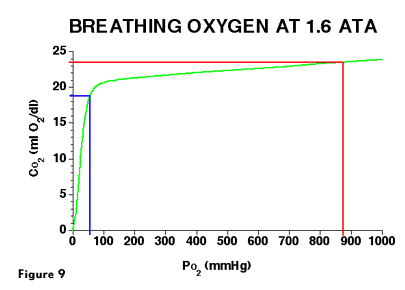
The a-v CO2 difference (vertical axis) remains constant at 4.5 mL O2/ dL blood. However, because dissolved oxygen content has been significantly increased, the CO2 values are shifted upward on the vertical axis, and the PO2 values are shifted to the right on the horizontal axis. Inspection of the curve in Figure 9 indicates that as CaO2 and CvO2 continue to move to the right, the oxygen window will continue to enlarge until CvO2 is shifted above the knee of the curve. This occurs when venous hemoglobin is fully saturated with O2, and only dissolved O2 is removed to supply tissue O2 demand. To achieve full saturation of venous hemoglobin requires an inspired PO2 of approximately 3 ATA.

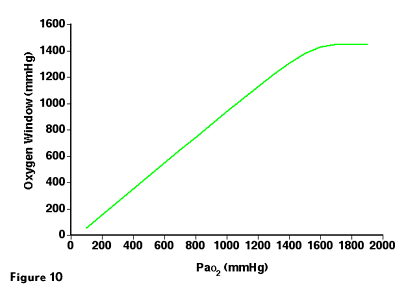
Figure 10 shows a plot of the oxygen window versus PaO2. When PaO2 exceeds 1600 mmHg, the oxygen window has reached a maximum value of 1400 mmHg. Above, this point, further increase in inspired PO2 will not increase the oxygen window. Oxygen toxicity clearly limits the oxygen window to much lower values during in water diving operations.

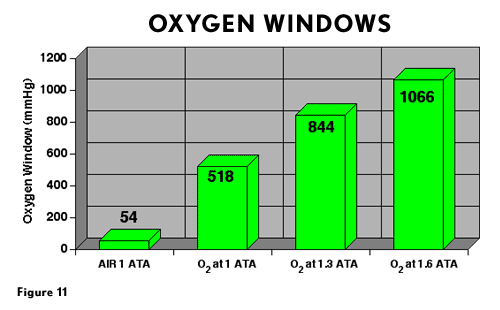
It is useful to consider what happens to the oxygen window when O2 is breathed at 10 and 20 FSW. Figure 11 shows oxygen windows for various circumstances. When O2 is breathed at 20 FSW (1.6 ATA), the oxygen window is 1066 mmHg. If O2 is breathed at 10 FSW (1.3 ATA), the oxygen window is reduced to 844 mmHg, a decrease of 222 mmHg. This means that there is less partial pressure vacancy in venous blood for non-metabolic gas to occupy during O2 breathing at 10 FSW as opposed to 20 FSW. Furthermore, inert gas elimination is independent of depth during oxygen breathing. The gas partial pressure gradient for movement from tissue into blood is not controlled by ambient pressure; it is controlled by the gas partial pressure in the tissue and in arterial blood. As long as the arterial gas partial pressure is zero, the gradient for gas removal from tissue is maximal. Breathing oxygen at a deeper depth has the advantage of a greater hydrostatic pressure to hold dissolved gas in solution.

If a gas mixture with less than 100% O2 were breathed, then some of the oxygen window would be occupied by the inert gas. For example, if a 50% or 80% Nitro mixture were breathed at 20 FSW, then N2 would occupy some of the partial pressure of the oxygen window. How much of the window would be occupied depends on the tissue N2 partial pressure, which will determine how much N2 would diffuse from blood into tissue and the resulting PvN2. The oxygen window would be reduced by an amount equal to the PvN2.

IS THE OXYGEN WINDOW IMPORTANT?
It should be intrinsically obvious that removal of a gas from tissue can be speeded by elimination of the gas from the inspired mixture. If the arterial partial pressure of a gas is zero, then no gas will diffuse into tissue while the gas is diffusing out of the tissue. As discussed above, diffusion of one gas in solution is not affected by the presence of other gases. Despite all of the above discussion of gas diffusion, most decompression models in common use, including Buhlmanns models, are perfusion-limited models. In such a model, diffusion is assumed to be infinite and thus cannot limit tissue gas uptake or removal. Tissue half-times for He and N2 are independent of each other, so the presence or absence of N2 does not change the rate of He on- or off-gassing and vise versa. In theory, He off-gassing should not be altered by breathing air, 50% Nitrox or 100% O2 during decompression from a He dive. He elimination during air or O2 decompression from a He-based dive has been measured, and the decompression gas did not affect the rate or volume of expired He (4). In another study at 1 ATA, tissue N2 washout is not different during O2 or Heliox breathing (3). Both studies are consistent with the physics of gas diffusion in solution, where the presence of a second non-metabolic gas does not slow diffusion of the first non-metabolic gas. The reality is that at any given ambient pressure, regardless of the size of the oxygen window, as long as there is no inspired He, the rate of He off-gassing will be unchanged.

Decompression from an N2-based dive is longer with N2 containing deco mixes because some N2 is continuously diffusing into tissue during deco. Decompression from a He-based dive can be longer with N2 containing deco mixes because N2 is diffusing into tissue as He is diffusing out of tissue. The decompression obligation of a tissue compartment is based on the sum of gas partial pressures in the compartment. This means that if a tissue is loaded with N2 as He is being removed, it tissue has a greater decompression obligation than when no N2 is added to tissue during He off-gassing. Enlarging the oxygen window can only occur when PaO2 is increased to a maximum tolerated value, either by increasing depth or increasing FiO2 of the gas mix, or both. Although enlarging the oxygen window may not directly affect tissue gas removal, it does directly affect tissue on-gassing during decompression, which affects the amount of time required to decompress the tissue.

Enlarging the oxygen window may have another effect, which is subtler than tissue on- or off-gassing. The following discussion is conjecture based on data available in the literature, and has not been directly studied. During decompression of animals from air dives, venous blood becomes supersaturated with N2 during the early stages of decompression, and venous blood supersaturation appeared related to venous bubble formation (2). Venous blood N2 supersaturation occurred following a relatively mild decompression stress of ascent from 33 FSW to surface. Once bubble formation had occurred, gas removal was slowed, possibly by bubbles in the venous circulation (2). By limiting the speed with which ambient pressure is changed, deep stops may function to limit venous blood supersaturation and limit bubble formation related to the supersaturation. Increasing the oxygen window during decompression will also limit venous blood supersaturation by limiting the amount of non-metabolic gas in blood. In essence, the presence or absence of a second non-metabolic gas will not alter the amount of gas evolved from tissue. However, the presence of an inspired non-metabolic gas could increase the severity of venous blood supersaturation.

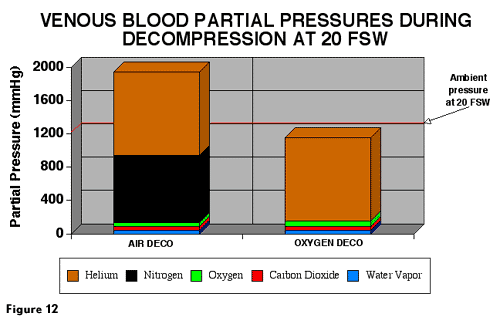
Figure 12 demonstrates hypothetical venous partial pressures during decompression from a He dive with either O2 or air at 20 FSW. In this example, the partial pressure of He in venous blood is assumed to be 1000 mmHg in both conditions. During air breathing at 20 FSW, PaN2 would be approximately 1140 mmHg, so an assumed PvN2 value of 800 mmHg allows some tissue N2 uptake. Ambient pressure at 20 FSW is 1216 mmHg. Due to the oxygen window, the total partial pressure in venous blood during O2 breathing would be 1150 mmHg, less than ambient. Total venous partial pressure during air breathing at 20 FSW would be 1937 mmHg, above ambient pressure. Although no direct experimental data exists on this topic, oxygen breathing may limit venous blood supersaturation, prevent venous bubble formation, and thus speed tissue gas removal.

CONCLUSIONS
It should be obvious from the above discussion that much decompression physiology is poorly understood, and models used at best approximate in vivo physiology. Clearly, not all decompression illness can be predicted or prevented. However, thoughtful application of available models coupled with careful diving technique can minimize risk of decompression illness. By reducing non-metabolic gas to a minimum and reducing tissue on-gassing, the oxygen window can be utilized to increase tissue off-gassing during decompression. Real life experience indicates that use of O2-enriched deco mixes can function to limit decompression time and possible the incidence of decompression illness. Use of high O2-mixes requires careful attention to dive planning and execution. As always, the careful, thoughtful diver will be the safer diver.

REFERENCES
Aksnes, E., and H. Rahn. Measurement of total gas pressure in blood. J. Appl. Physiol. 10: 173-178, 1957.2.

DAoust, B. G., H. T. Swanson, R. White, R. Dunford, and J. Mahoney. Central venous bubbles and mixed venous nitrogen in goats following decompression. J. Appl. Physiol. 51: 1238-1244, 1981.3.

Groom, A. C., S. H. Song, Y. Ohta, and L. E. Farhi. Effect of anesthesia on rate of N2 washout from body stores. J. Appl. Physiol. 37: 219-223, 1974.4.

Kindwall, E. P. Measurement of helium elemination from man during decompression breathing air or oxygen. Undersea Biomed. Res. 2: 277-284, 1975.5.

Krogh, A., and M. Krogh. On the tension of gases in the arterial blood. Skandinavisches Archiv f r Physiologie 23: 179-192, 1910.6.

Lategola, M. T. Measurement of total pressure of dissolved gas in mammalian tissue in vivo. J. Appl. Physiol. 19: 322-324, 1964.7.

Vann, R. D., and E. D. Thalmann. Decompression Physiology and Practice In P. Bennett and D. Elliott (eds): The Physiology and Medicine of Diving. London, W. B. Saunders Company, Ltd., 1993, pp 376-432